DeepSeek AI has announced the launch of DeepSeek-Prover-V2, an innovative open-source large language model designed specifically for formal theorem proving within the Lean 4 environment. This new version builds on previous developments by introducing a novel recursive theorem-proving pipeline. It utilizes the capabilities of DeepSeek-V3 to generate its own high-quality initialization data. As a result, the model achieves state-of-the-art performance in neural theorem proving. Alongside this release, DeepSeek AI has also introduced ProverBench, a new benchmark aimed at evaluating mathematical reasoning skills.
One of the key breakthroughs in DeepSeek-Prover-V2 is its unique cold-start training method. This process starts by prompting the powerful DeepSeek-V3 model to break down complex mathematical theorems into a series of smaller, more manageable subgoals. At the same time, DeepSeek-V3 formalizes these high-level proof steps within Lean 4, effectively creating a structured sequence of sub-problems. This approach helps organize the proof process into clear, incremental steps.
To manage the computationally demanding proof search for each subgoal, the researchers used a smaller 7 billion parameter model. Once all the decomposed steps of a difficult problem are successfully proven, the complete step-by-step formal proof is paired with DeepSeek-V3’s corresponding chain-of-thought reasoning. This clever strategy enables the model to learn from a synthesized dataset that combines informal, high-level mathematical reasoning with rigorous formal proofs. This provides a strong foundation, or cold start, for subsequent reinforcement learning.
Building on this synthetic cold-start data, the DeepSeek team selected a set of challenging problems that the 7B prover model could not solve entirely on its own. However, all the subgoals within these problems had been successfully addressed. By combining the formal proofs of these subgoals, a complete proof for the original problem is constructed. This formal proof is then linked with DeepSeek-V3’s chain-of-thought, which outlines the lemma decomposition. This creates a unified training example that begins with informal reasoning and is followed by formalization.
The prover model is then fine-tuned using this synthetic data. After fine-tuning, it undergoes a reinforcement learning phase. During this phase, binary feedback indicating whether a proof is correct or incorrect serves as the reward signal. This process further refines the model’s ability to bridge the gap between informal mathematical intuition and the precise construction of formal proofs.
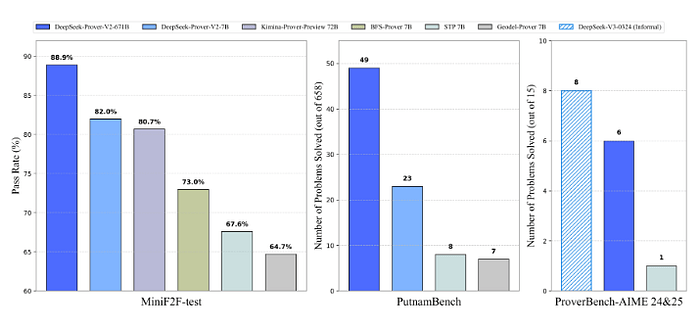
The result of this innovative training pipeline is DeepSeek-Prover-V2–671B, a model with 671 billion parameters. This model has demonstrated outstanding results, achieving state-of-the-art performance in neural theorem proving. It reached an impressive 88.9% pass ratio on the MiniF2F-test and successfully solved 49 out of 658 problems from PutnamBench. The proofs generated by DeepSeek-Prover-V2 for the MiniF2F dataset are publicly available for download, allowing researchers and practitioners to examine and analyze them further.
In addition to the model release, DeepSeek AI has introduced ProverBench, a new benchmark dataset consisting of 325 problems. This benchmark is designed to provide a more comprehensive evaluation of mathematical reasoning abilities across various difficulty levels. ProverBench includes 15 problems formalized from recent AIME (American Invitational Mathematics Examination) competitions, specifically AIME 24 and 25. These problems offer authentic challenges at the high-school competition level. The remaining 310 problems come from carefully selected textbook examples and educational tutorials. This diverse collection covers a wide range of formalized mathematical problems from different areas, making ProverBench a valuable tool for assessing neural theorem provers on both challenging competition problems and fundamental undergraduate-level mathematics.
DeepSeek AI is releasing DeepSeek-Prover-V2 in two model sizes to accommodate different computational resources. The smaller model has 7 billion parameters, while the larger one contains 671 billion parameters. DeepSeek-Prover-V2–671B is built on the strong foundation of DeepSeek-V3-Base. The smaller DeepSeek-Prover-V2–7B model is based on DeepSeek-Prover-V1.5-Base and features an extended context length of up to 32,000 tokens. This extended context length allows it to process longer and more complex reasoning sequences.
The release of DeepSeek-Prover-V2, together with the introduction of ProverBench, represents a significant advancement in the field of neural theorem proving. By leveraging a recursive proof search pipeline and providing a challenging new benchmark, DeepSeek AI is enabling the research community to develop and evaluate more sophisticated and capable AI systems for formal mathematics.